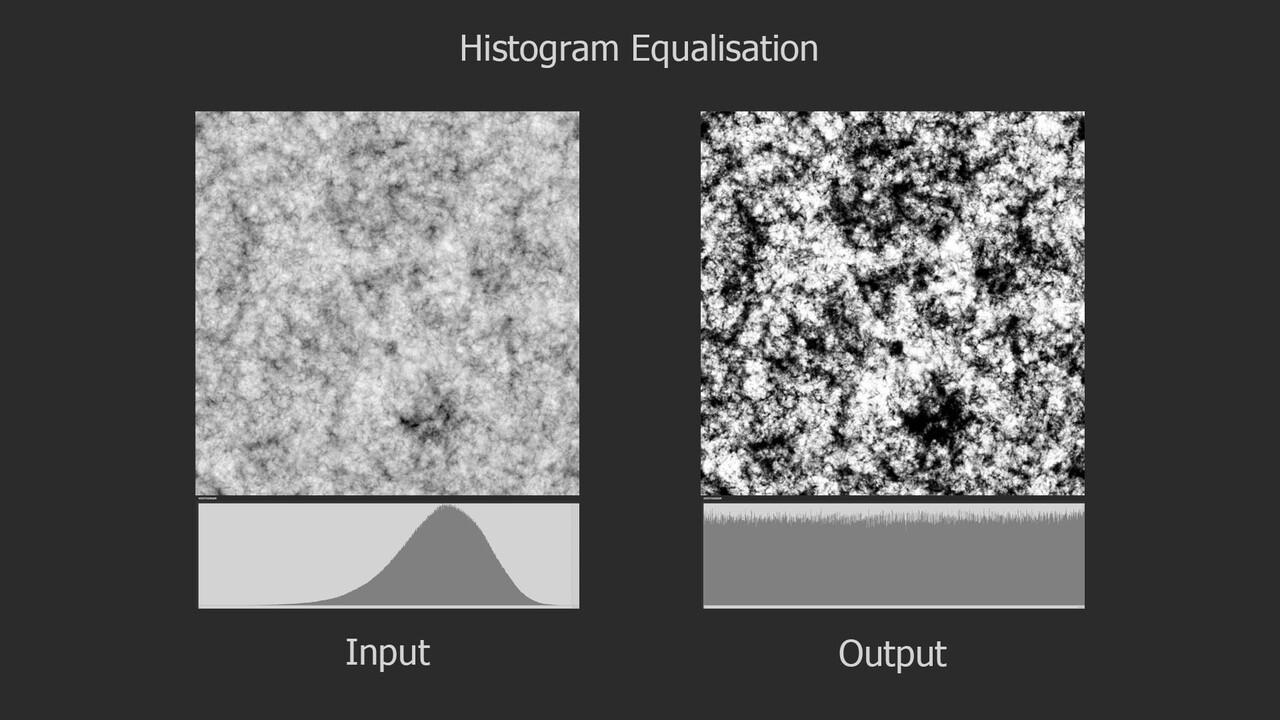
In my last blog post, we explored the fundamentals of histogram equalization. If you have not read that yet, you may want to do so first as this post is a direct continuation of that. Here we begin the practical implementation in Substance Designer itself. Initially, I planned to cover the entire process in one go, but due to its complexity, I've decided to break it down into segments. So in this installment, we'll focus exclusively on computing the Probability Density Function (PDF).

I will assume you have some familiarity with Substance Designer's FXMap, as I won't go into its basics here. There is simply too much to cover about the node and CGVinny (who works at Substance) has done great resources on that topic already. My aim is to provide us with a clear understanding of PDF computation and a visual understanding of the function graph itself. While knowledge of the FXMap isn't critical, it will help. So, let's get started.

The histogram equalization node consists of three main components: PDF computation, Cumulative Distribution Function (CDF) computation, and value remapping. We will focus on the PDF node.

While the actual node you can download contains multiple setups for varying bin counts, we'll simplify things here by focusing on a 16-bin example. Trying to visualize and animate more than 16 is difficult! In the downloadable node, you'll find four different bin configurations: 64, 128, 256, and 1024 bins. However, the computational approach remains the same across these variations.

Probability Density Function (PDF) in Designer

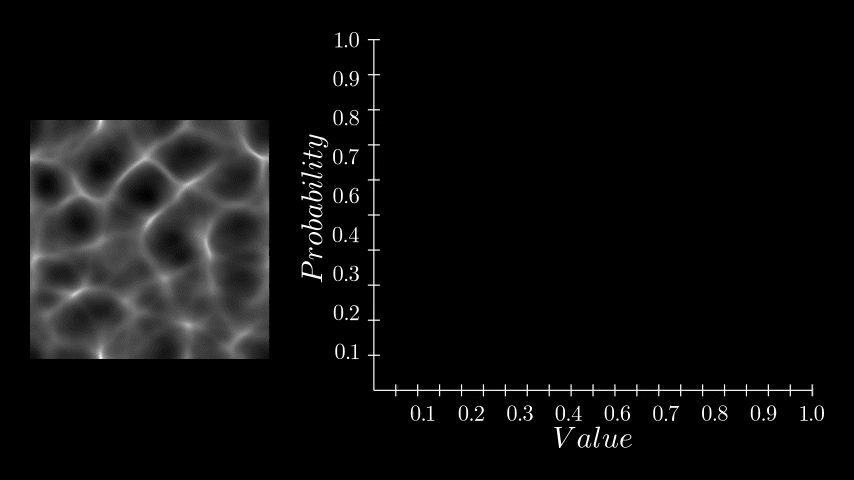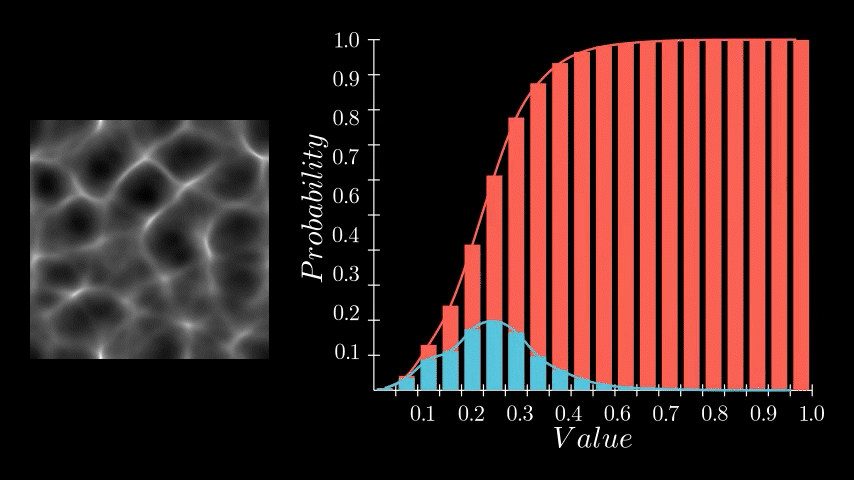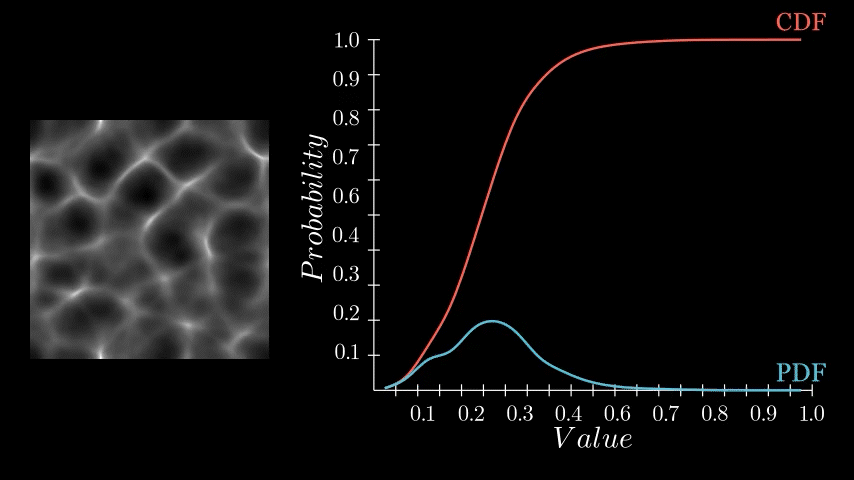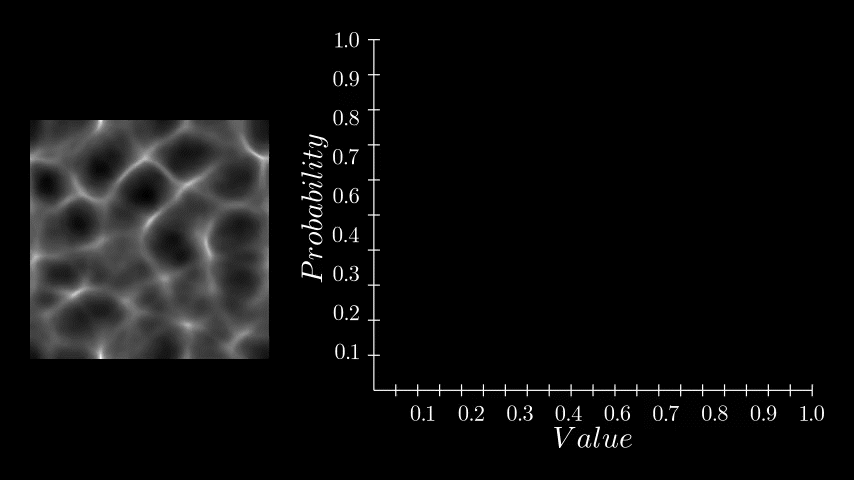
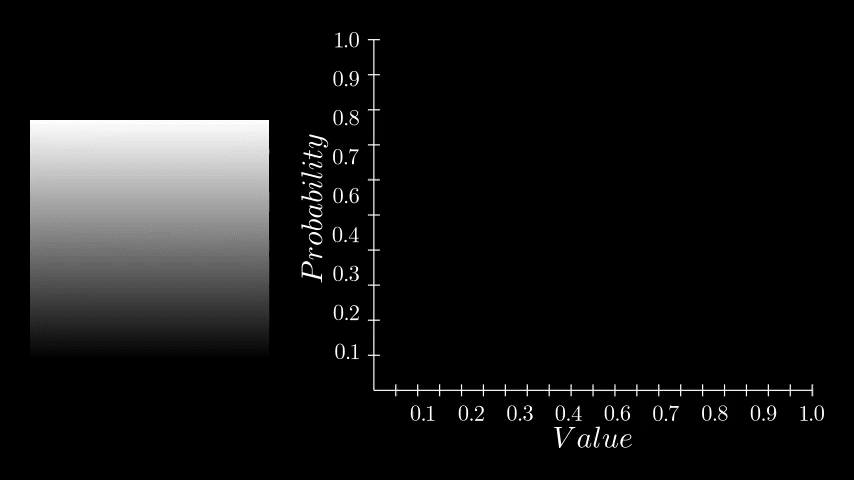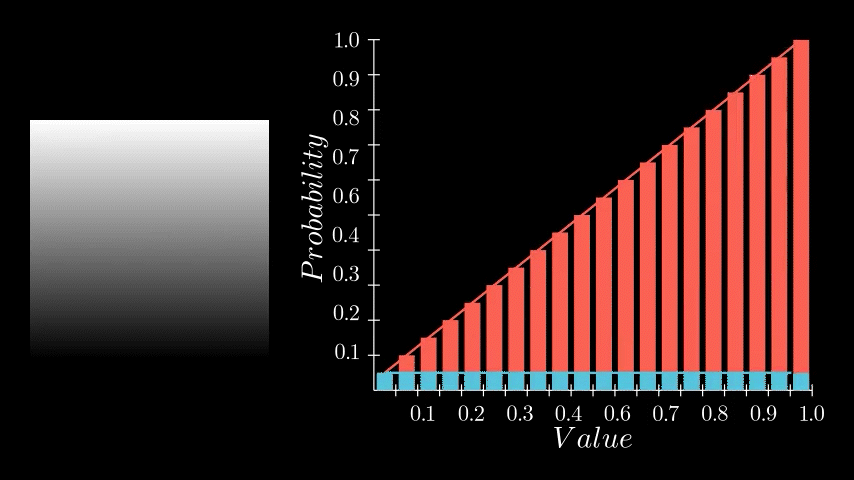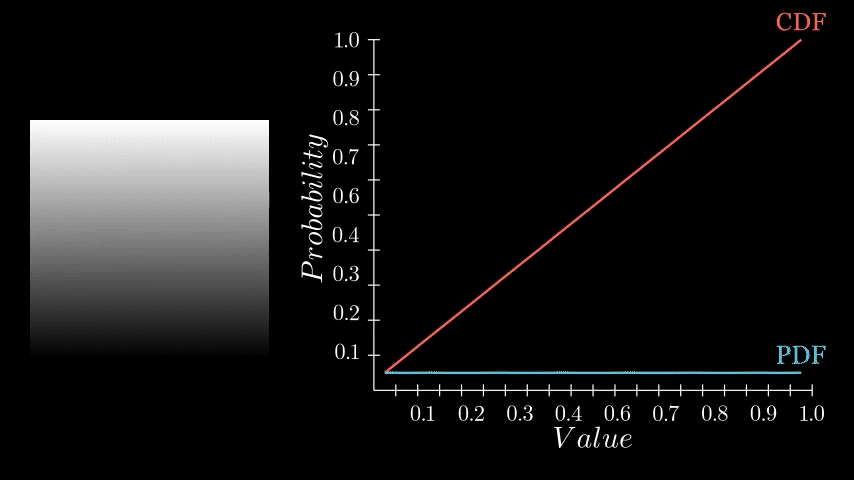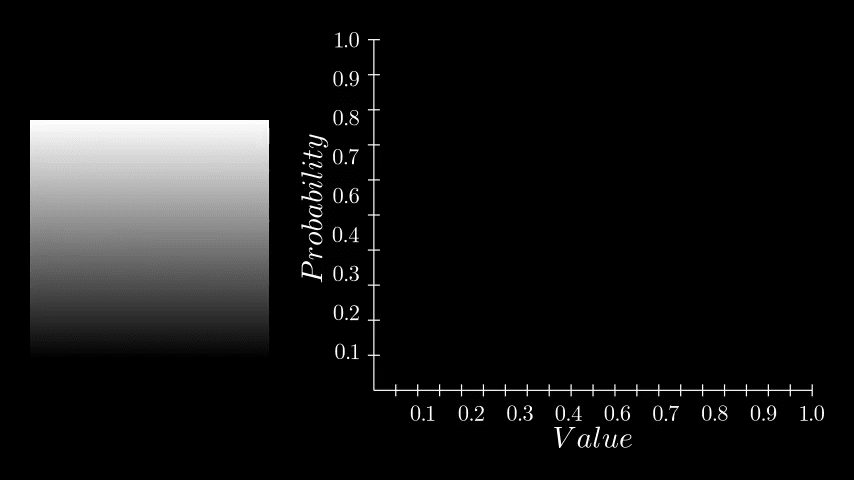
If you recall, the PDF represents the likelihood of each pixel intensity value appearing in the image. We previously saw this as either a graph with bars or a continuous function but in Substance Designer, we don't have those representations available to us. Instead, we need to store it as a 1x16 image, with each pixel's value corresponding to the probability of its respective bin along the horizontal. The entire goal in this post is to generate this 1x16 image. We are aiming to eventually build a Look Up Table (LUT) that will remap our original pixel values to the Cumulative Distribution Function (CDF) and this is pixel strip containing PDF values is the first step in that. In the released node, this means generating a 1x64, 1x128, 1x256, and 1x1024 image respectively.

To generate our PDF, we use the FXMap, connecting multiple Quadrant nodes to subdivide the image into 16x16 squares. These squares serve as our 'samples'. Using their coordinates, we sample the image pixel values, which are then categorized into bins and counted to produce our PDF image. Sounds confusing in words but check the animation below. The process will work like this:

• Sub divide: Image will be sub divided into adequate resolution.
• Sampling: Use the sample position to get the pixel value at that location
• Value binning: pixel values will be modified so they fall into a bin.
• Bin assignment: Samples are moved into a new designated bin location along the horizonal
• Aggregation: Samples with identical pixel values end up in the same location, making counting straightforward.

To actually count the pixels, each sample in the image will be repositioned based on its pixel value. This repositioning moves a sample into a predefined location, somewhere else in the texture, with the idea being that samples with the same pixel value will move to the same location, providing us a means to count them. We can have the bin locations next to each other running horizontal, starting from pixels with a value of 0 through to 1. While the animation below shows the strip to the right, it will actually be placed at the top of the image, which you will see shortly.

With our approach outlined, let's delve into the actual implementation. The core logic resides on the intensity parameter of a quadrant node in the FXMap, nested within the node structure.

While there are additional nodes in the PDF graph, they relate to optimization and are not pivotal to our discussion. Our main focus will be on the function graph depicted below:

Binning

The first part of this function graph I want to talk about is value binning.

Our plan is to relocate every sample to its predefined location at the top of the image. To achieve this, we employ a process called 'binning', where each pixel value gets assigned to one of these 16 locations. Binning is accomplished through a method known as quantization. This process aligns each pixel value with a corresponding bin increment. We implement it as follows:

• First, for every sample, we get its intensity value using its position within the texture. This value will range between [0:1].
• We then multiply this intensity by 16 which is required for the next step to work.
• Next, we apply a flooring operation. This step effectively rounds down the result to the nearest whole number, aligning each pixel value with the nearest bin increment.
• Finally, we rescale the floored value back into the original range of [0:1]. This rescaling ensures that our quantized value stays within the original intensity range.

This quantization process effectively 'snaps' each pixel value to one of the 16 bin increments, which in turn will correspond to its new bin location along the horizonal. Think of this new value as an offset.

Repositioning

Moving the sample is done as follows:

• Use the position variable to get the coordinates for each sample.
• Negate the coordinates to move the sample to the origin.
• Add the binned pixel value to offset it to the correct location.

The negation process effectively resets each sample's position back to the image's origin point, which in Substance Designer is the top left corner (0,0), This is the reason why we are building the strip at the top. By subtracting the original position values from each sample, we align them all back to the origin. We then add the binned pixel value to each sample, offsetting it into its respective bin based on its intensity.

Counting

Once the samples are moved into their respective bins, they stack on top of one another. To count them, we could force each sample's pixel value to 1 (and set the FXMap node to add/sub). This configuration means that as samples of the same pixel value stack in each bin, their new value which we have set to 1 accumulates, effectively counting the number of samples in each bin. The stacked total at each bin then represents the count of samples for that bin's intensity range.

Normalization

Having determined the counts for each bin, we can now compute the final PDF. This involves normalizing the counts. We do this by dividing each bin's count by the total number of samples. In our example, since our sample grid was 16x16, the total is 256 samples. Dividing by the sample count gives us the probability of each bin. A small detail in this implementation is that this normalization is performed incrementally for each sample during the counting process, rather than as a separate step after all counts are tallied. This was done for simplicity sake but can happen during of after counting.

And thats it! We now have a strip of pixels who values represent the PDF of that image. All that remains is to crop out this little strip and there we go.

One key point to consider is the impact of sample resolution on PDF accuracy. A low sample count, like our 16x16 example, offers a very crude approximation of the texture's actual distribution, especially with high resolution such as 2048 or 4096 . In the actual implementation of the node, this process happens with 64, 128, 256 or 1024 bins, rather than just 16 but even with only 64 bins the accuracy is surprisingly good.

From my testing, increasing the bin count beyond 256 didn't offer much benefit in terms of accuracy, especially considering the additional computational cost. In fact, this method becomes impractically slow with anything beyond 1024 bins. Therefore, I found 256 bins to be an optimal balance between accuracy and performance and a good default value.

I hope this explanation has provided some understanding of the PDF computation and its practical implementation. Should you have any questions, thoughts, or feedback, feel free to reach out.

In precedent with my other Substance Nodes, this blog will accompany the Histogram Equalization node. It will be a two part series going through the node; how it works from underlying theory to Substance Designer implementation.

NOTE: Adobe has implemented histogram equalization natively into the program since writing these posts.

First we will discuss histogram equalization, then in part two, we will cover the Substance Designer implementation.

If you don't know what it is, you can think of it as a kind of contrast adjustment for an image. Somewhat like doing an levels adjustment or using the existing histogram nodes in Designer.

However, equalization is actually something quite different. Here is a more formal definition: Histogram equalization is a technique used to redistribute the intensity values of an image so that they are uniformly spread across the available range (typically 0 to 255 for an 8-bit image). The goal is to make the histogram of the modified image as flat as possible, meaning that each intensity value is equally probable.

If any of that did not make sense to you don't worry, hopefully it will by the end of this post. So lets begin with understanding what a histogram is exactly and why we might want to equalize it.

A histogram is a graphical representation of the distribution of pixel values within a texture. The x-axis shows the range of pixel values, and the y-axis is a count of how many pixels had those values in the image. Visually, a histogram is often used to understand the characteristics of a texture, such as brightness or value range. Programmatically, a histogram is often used to analyze and adjust the contrast, brightness, and overall tonal balance of the image.

For our histogram below, these values are grouped into 20 evenly spaced 'bins' for easier viewing (but is it common to use 256). Then each pixel value which falls into a bin, is counted.

If you divide the histogram counts by the total number of pixels in the image (a process known as normalization) and draw a continuous curve through the points, this is called a Probability Density Function (PDF). The PDF tells you the probability of a pixel having a particular value.

While a histogram provides discrete counts, a PDF gives you a continuous probability curve, a subtle but important difference. In the context of everyday 3D art and textures, they can be used interchangeably, but it's important to understand the subtle differences between them since one speaks about counts and the other probability.

If you have spent any time with Substance Designer, you have likely seen the histogram. Typically we use nodes like histogram range or auto levels as a way to manipulate it, however unlike those nodes, which are linear operations (meaning your just moving the histogram up, down or stretching it), equalization completely redistributes the values in the image, changing the profile of the histogram itself. In the image below, notice how the linear operations maintain the bell shaped hump in the center, while the equalization changed the profile completely.

In the context of texturing, this can be incredibly helpful for all kinds of things. A common use case could be for generating color information with a gradient map or my color nodes (shameless plug). Equalizing the input image will ensure that you sample the full range of colors and not bias it to a small region of the color gradient.

If you cumulate the histogram, by going through each bin, summing the count from the bin before, you create what is called a Cumulative Distribution Function (CDF).

This function represents the probability that a pixel will have a value less than or equal to a given number. Unlike a Probability Density Function, which shows the probability of a pixel having a specific value, the CDF shows cumulative probabilities. It is not often you will come across a CDF in day to day texture work, but in the context of image processing, this information can be very useful and as you may have guessed, it is crucial for performing histogram equalization.

Lets look at some histograms to familiarize ourselves with how both PDF and CDF looks for difference types of images.

In the image below, we have a relatively mid tone image where most of the pixels are floating around the mid range. Notice how you can see this behavior represented both in the PDF with its hump in the center and the CDF transitioning sharply in the same location.

In the next image, the values are mostly residing in the upper range, which moves everything up in the PDF and CDF also.

While a darker image pushes everything to the lower range.

One very important PDF/CDF is that of an image where every pixel is equally likely. Such as a linear gradient.

Notice here that each histogram bin has exactly the same count, thus each pixel value has the same probability of occurring, which in turn means the CDF is a perfectly straight line. Why this is the case is essential to understanding equalization, so take a moment to think on it if it feels ambiguous. Here the CDF is saying that each pixel value (x axis) has the same cumulative probability (y axis). Or, put in other words, by half way through the value range (x axis), I will have seen exactly 50% of the values (y axis). Or, by value 0.75, I will have seen exactly 75% of the values and so on.

Histogram equalization works by remapping the image pixel values according to its CDF. What that means in practice is computing a CDF for the image then replacing each pixel value with the corresponding CDF value.

If you were like me, this seemed incredibly simple, but also...what?! Sure, remapping pixel values is straightforward (gradient dynamic node in Substance), take one value and convert it to another based on that function, but it was not at all clear to me why remapping with the CDF would work, much less one generated from the image itself.

To better understand this, consider the transformation as a function, let's call it f(x). In this equation, x is the input image, and the output we want to be the remapped equalized image. It's logical to assume that f(x) would be related to probabilities, after all we are trying to equalize the image and the CDF does indeed provide a probability distribution for the image. But still, it wasn't clear to me why this works. I did not have an intuition or clear visualization of what was happening.

Recall, the CDF tells you the probability that a randomly picked pixel will have a certain intensity value or lower.

When remapping, I like to visualize it as projecting that CDF curve onto the x=y line. This line also happens to be what a perfectly equalized image CDF looks like, as we saw before.

This projection is essentially saying something like "we want 80% of the pixels to have occurred by value 0.8, not 0.27 which is where it was before". This is why using the CDF works, its taking all the probability information in the image, and forcing it to be linear.

That's all there is to it really. It is a single remapping from one set of values to another but all the mystery and magic comes from those set of numbers containing information about the pixel value probabilities.

And that concludes the first part of our jump into histogram equalization, I hope it was useful. In the next part of this series, we will go through how this can be implemented in Substance Designer.